Трикутна призма: скільки граней і як їх порахувати

Уявіть собі тривимірну геометричну фігуру, яка немов би витягує трикутник у простір, створюючи об’ємну форму, що зачаровує своєю простотою та елегантністю. Це трикутна призма – багатогранник, який часто з’являється в задачах із геометрії, архітектурі чи навіть у повсякденних предметах, як-от скляні брелоки чи оптичні прилади. Але скільки граней має ця загадкова фігура? І чому це питання таке важливе? У цій статті ми зануримося в геометричний світ трикутної призми, розкриємо її секрети та пояснимо все настільки детально, що навіть новачок відчує себе експертом.
Що таке трикутна призма?
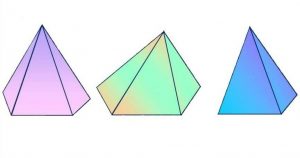
Трикутна призма – це багатогранник, який складається з двох паралельних трикутних основ і трьох бічних граней, що з’єднують їх. Уявіть два однакових трикутника, які лежать у паралельних площинах, а між ними – три поверхні, що нагадують стіни будинку. Ця геометрична фігура належить до сімейства призм, назва яких походить від грецького слова «πρίσμα» – «відпиляне». І справді, трикутна призма виглядає так, ніби її акуратно вирізали з більшого шматка простору.
Основна особливість трикутної призми – її простота та універсальність. Вона може бути прямою (коли бічні грані перпендикулярні до основ) або похилою (коли грані нахилені). Якщо основи – рівносторонні трикутники, а бічні грані – прямокутники, ми маємо справу з правильною трикутною призмою, яка є справжньою зіркою геометрії завдяки своїй симетрії.
Скільки граней у трикутної призми?
Трикутна призма має п’ять граней: дві трикутні основи та три бічні грані, які зазвичай є прямокутниками в прямій призмі або паралелограмами в похилій. Це число – ключ до розуміння структури призми, адже воно визначає її форму та властивості.
Щоб краще це уявити, подумайте про скляну призму, яка розкладає світло на веселку. Її трикутні основи – це «обличчя» фігури, а бічні грані – «тіло», яке з’єднує ці обличчя. Кількість граней завжди однакова, незалежно від розміру чи типу трикутника в основі.
Чому саме п’ять граней?
Логіка проста, але захоплива. Дві грані – це трикутні основи, які завжди паралельні та конгруентні (тобто однакові за формою і розміром). Решта три грані – це поверхні, які з’єднують відповідні сторони цих трикутників. Кожна сторона трикутника породжує одну бічну грань, а оскільки трикутник має три сторони, ми отримуємо три бічні грані. Разом: 2 (основи) + 3 (бічні грані) = 5 граней.
Ця структура робить трикутну призму пентаедром – багатогранником із п’ятьма гранями. Цікаво, що трикутна призма є найпростішим представником призм, адже має найменшу кількість граней серед усіх призм із багатокутними основами.
Елементи трикутної призми: вершини, ребра, грані
Щоб зрозуміти трикутну призму, варто розібратися не лише з гранями, а й з іншими її елементами. Кожен елемент – це частина пазла, який формує цілісну картину.
- Грані: Як ми вже з’ясували, їх п’ять – дві трикутні основи та три бічні грані.
- Вершини: Кожна основа – це трикутник із трьома вершинами. Оскільки призма має дві основи, загалом отримуємо 6 вершин (3 × 2).
- Ребра: Трикутна призма має 9 ребер: 3 ребра на кожній основі (3 × 2 = 6) плюс 3 бічні ребра, які з’єднують відповідні вершини основ.
Ці числа пов’язані між собою теоремою Ейлера для опуклих багатогранників: Вершини + Грані − Ребра = 2. Для трикутної призми: 6 + 5 − 9 = 2. Це підтверджує правильність наших підрахунків і додає геометрії нотку магії, чи не так?
Типи трикутних призм: прямі, похилі, правильні
Не всі трикутні призми однакові. Вони можуть відрізнятися за формою, кутом нахилу чи типом основи. Розглянемо основні різновиди, щоб зрозуміти, як це впливає на кількість граней.
Пряма трикутна призма
У прямій призмі бічні грані перпендикулярні до основ, що робить їх прямокутниками. Це найпоширеніший тип, який легко уявити: трикутник «витягується» вгору, утворюючи чітку, струнку форму. Кількість граней залишається п’ятьма, але форма бічних граней додає фігурі геометричної строгості.
Похила трикутна призма
У похилій призмі бічні грані не перпендикулярні до основ, а нахилені, через що вони стають паралелограмами. Це додає фігурі динаміки, ніби вона нахилилася під поривом вітру. Кількість граней не змінюється – їх усе ще п’ять, але обчислення площі чи об’єму стають складнішими через нахил.
Правильна трикутна призма
Правильна трикутна призма – це пряма призма з рівносторонніми трикутниками в основі та прямокутними бічними гранями. Її симетрія заворожує: усі сторони основи рівні, а кути становлять 60°. Така призма ідеально вписується в циліндр, що робить її улюбленицею в задачах із геометрії.
Незалежно від типу, кількість граней завжди дорівнює п’яти. Але форма граней і їхні властивості впливають на розрахунки та практичне застосування.
Як порахувати площу та об’єм трикутної призми?
Трикутна призма не лише гарна, а й практична. Її грані та розміри дозволяють обчислити площу поверхні та об’єм, що корисно в задачах із геометрії чи інженерії.
Площа поверхні
Площа поверхні трикутної призми – це сума площ двох основ і трьох бічних граней. Для прямої призми формула виглядає так:
S = 2 × Sосн + Sбіч
Де Sосн – площа трикутної основи, а Sбіч – сума площ бічних граней. Для правильної призми з рівностороннім трикутником в основі площу основи можна обчислити за формулою:
Sосн = (a² × √3) / 4, де a – сторона трикутника.
Бічні грані в прямій призмі – прямокутники, тож їхня площа дорівнює добутку довжини сторони основи на висоту призми.
Об’єм
Об’єм трикутної призми обчислюється як добуток площі основи на висоту призми:
V = Sосн × h
Для похилої призми висота – це перпендикуляр між основами, що може ускладнити розрахунки, адже вона не збігається з бічним ребром.
Практичне застосування трикутної призми
Трикутна призма – не просто абстрактна геометрична фігура, а й об’єкт, який ми бачимо в реальному житті. Ось кілька прикладів її використання:
- Оптика: Скляні призми використовують для розкладання світла на спектр, що допомагає вивчати властивості світла.
- Архітектура: Трикутні призми надихають на створення міцних конструкцій, як-от дахи будинків чи мости.
- Дизайн: Від брелоків до сучасних світильників – форма призми додає естетики та функціональності.
Розуміння кількості граней допомагає інженерам і дизайнерам точно розраховувати матеріали чи аналізувати міцність конструкцій.
Порівняння трикутної призми з іншими багатогранниками
Щоб глибше зрозуміти трикутну призму, порівняймо її з іншими багатогранниками. Ось таблиця, яка ілюструє основні відмінності:
| Фігура | Кількість граней | Кількість вершин | Кількість ребер |
|---|---|---|---|
| Трикутна призма | 5 | 6 | 9 |
| Чотирикутна призма | 6 | 8 | 12 |
| Тетраедр | 4 | 4 | 6 |
Джерело: mathros.net.ua
Трикутна призма вирізняється своєю компактністю порівняно з іншими призмами, але поступається за кількістю граней, наприклад, кубу чи чотирикутній призмі.
Цікаві факти про трикутну призму
Трикутна призма – це не лише геометрична фігура, а й джерело цікавих фактів, які роблять її ще більш захопливою:
- Трикутна призма є пентаедром – багатогранником із п’ятьма гранями, що робить її унікальною в сімействі призм.
- У природі трикутні призми можна побачити в кристалах, наприклад, у кварці чи кальциті.
- Скручена трикутна призма (многогранник Шенхардта) не може бути розбита на тетраедри без додавання нових вершин, що робить її геометричною загадкою.
Ці факти показують, що трикутна призма – це не просто набір граней, а цілий світ геометричних відкриттів.
Як трикутна призма використовується в освіті?
У школах трикутна призма – один із перших багатогранників, який вивчають на уроках геометрії. Вона допомагає учням зрозуміти поняття об’єму, площі поверхні та зв’язок між двовимірними й тривимірними фігурами.
Наприклад, задачі на обчислення площі чи об’єму призми вчать учнів працювати з формулами та розвивають просторову уяву. А розгортка призми – двовимірне зображення всіх її граней – допомагає зрозуміти, як тривимірна фігура «розкладається» на площині.
Трикутна призма – це не просто геометрична абстракція, а місток між теорією та реальним світом. Її п’ять граней, шість вершин і дев’ять ребер створюють гармонійну структуру, яка надихає на дослідження та творчість. Чи то в задачах із геометрії, чи в архітектурних проєктах, ця фігура залишається універсальним інструментом для розуміння простору навколо нас.