Що таке гострий кут: вичерпний гайд для всіх

Гострий кут — це не просто геометрична абстракція, а жива частинка світу математики, яка ховається в трикутниках, зірках на небі та навіть у кутках наших будинків. Уявіть собі розкритий зошит, де сторінки утворюють кут, менший за ідеально прямий — ось це і є гострий кут! У цій статті ми зануримося в усі аспекти гострого кута: від його визначення до практичного застосування, розкриємо його властивості та поділимося цікавими фактами, які зроблять геометрію ближчою і зрозумілішою.

Визначення гострого кута: основи, які варто знати

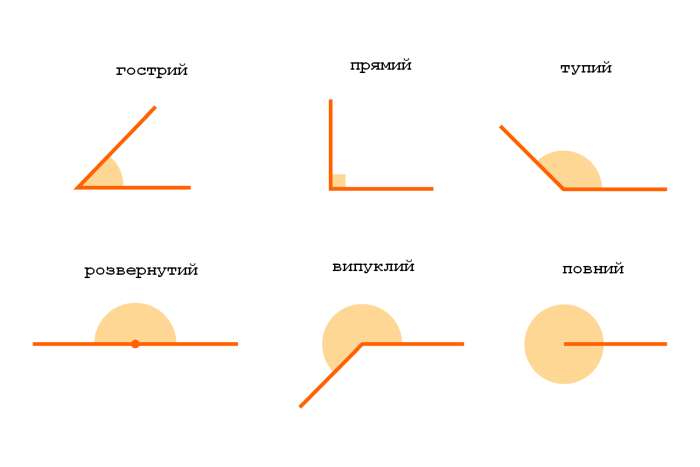
Гострий кут — це геометрична фігура, утворена двома променями, що виходять із однієї точки, яку називають вершиною кута. Його особливість у тому, що величина такого кута завжди менша за 90 градусів. Якщо уявити годинник, то гострий кут — це, наприклад, кут між стрілками, коли годинник показує 10:00, адже промені розходяться не надто широко.

У планіметрії гострий кут є однією з основних будівельних цеглинок геометричних фігур. Він визначається як простір між двома променями, які мають спільну початкову точку. Величина кута вимірюється в градусах (°) або радіанах, але для простоти ми зосередимося на градусах. Наприклад, кут у 30° або 60° — це завжди гострий кут, адже він менший за прямий кут (90°).

Щоб краще зрозуміти, уявіть собі трикутник. Якщо всі його кути менші за 90°, це гострокутний трикутник. Такий трикутник виглядає “гострим” і компактним, на відміну від “розлогого” тупокутного трикутника, де один кут перевищує 90°.

Як вимірювати гострий кут: інструменти та методи

Вимірювання гострого кута — це як спроба зловити момент, коли стрілки годинника утворюють ідеальну картинку. Основний інструмент для цього — транспортир. Цей півкруглий прилад із позначками градусів дозволяє точно визначити величину кута.

Ось як виміряти гострий кут за допомогою транспортира:

1. Розташуйте транспортир: Покладіть центр транспортира (маленьку позначку в основі) на вершину кута.
2. Вирівняйте одну сторону: Переконайтеся, що одна сторона кута збігається з нульовою позначкою транспортира.
3. Зчитайте значення: Подивіться, де друга сторона кута перетинає шкалу транспортира. Число, яке ви побачите, і є величиною кута в градусах.
4. Перевірте результат: Якщо кут менший за 90°, вітаємо — ви виміряли гострий кут!

Після вимірювання ви можете перевірити, чи кут дійсно гострий, порівнявши його з прямим кутом. Наприклад, якщо транспортир показує 45°, це однозначно гострий кут. Для точнішого вимірювання в геометрії іноді використовують мінути (1° = 60′) і секунди (1′ = 60″), але для більшості задач достатньо градусів.

Гострий кут у трикутниках: ключ до геометричної гармонії

Гострий кут відіграє особливу роль у трикутниках, адже він визначає їхній тип і властивості. У гострокутному трикутнику всі три кути менші за 90°. Це робить таку фігуру компактною, а її сторони — пропорційно збалансованими. Наприклад, рівносторонній трикутник, де кожен кут дорівнює 60°, є класичним прикладом гострокутного трикутника.

Цікаво, що в гострокутному трикутнику ортоцентр (точка перетину висот), центроїд (точка перетину медіан) і центр описаного кола завжди розташовані всередині трикутника. Це відрізняє його від тупокутного трикутника, де ортоцентр і центр описаного кола можуть бути зовні.

Ось таблиця, яка порівнює гострокутні та інші типи трикутників за їхніми кутами:

Тип трикутника	Характеристика кутів	Приклад кутів
Гострокутний	Усі кути < 90°	30°, 60°, 60°
Прямокутний	Один кут = 90°	90°, 45°, 45°
Тупокутний	Один кут > 90°	120°, 30°, 30°

Джерело: Загальні принципи геометрії, викладені на основі шкільних підручників.

Ця таблиця допомагає зрозуміти, як гострі кути впливають на форму трикутника. Гострокутні трикутники часто асоціюються з гармонією, адже їхні кути не “розтягують” фігуру надто сильно.

Властивості гострого кута: що робить його особливим?

Гострий кут має кілька унікальних властивостей, які роблять його незамінним у геометрії:

• Менший за 90°: Це основна ознака, яка визначає гострий кут. Наприклад, кут у 45° або 60° завжди гострий.
• Суміжність із тупим кутом: Якщо два кути суміжні (мають спільну сторону і вершину), і один із них гострий, то другий обов’язково тупий, адже їхня сума дорівнює 180°.
• Вертикальні кути: Якщо два гострі кути є вертикальними (утворюються при перетині двох прямих), вони завжди рівні. Наприклад, якщо один кут дорівнює 30°, то вертикальний до нього кут також буде 30°.
• Тригонометричні функції: У гострокутних трикутниках синус, косинус і тангенс кутів завжди позитивні, що спрощує обчислення.

Ці властивості роблять гострі кути ключовими у розв’язанні геометричних задач. Наприклад, у тригонометрії гострі кути часто використовуються для обчислення відстаней і висот, адже їхні тригонометричні значення простіші для роботи.

Гострий кут у реальному житті: де ми його бачимо?

Гострі кути оточують нас скрізь, навіть якщо ми не завжди їх помічаємо. Вони ховаються в архітектурі, природі та навіть у повсякденних предметах. Ось кілька прикладів, де гострі кути відіграють важливу роль:

• Архітектура: У конструкціях мостів гострі кути в трикутних фермах забезпечують міцність і стійкість.
• Дизайн: У сучасних меблях, як-от кріслах із гострокутними ніжками, ці кути додають естетики та стабільності.
• Природа: Листя багатьох рослин, наприклад, клена, мають гострокутні форми, що допомагають оптимізувати поглинання світла.
• Технології: У складних механізмах, як-от шестерні, гострі кути забезпечують точність і ефективність.

Ці приклади показують, що гострі кути — це не просто абстрактна геометрія, а частина нашого світу, яка впливає на його функціональність і красу.

Цікаві факти про гострі кути

Ось кілька захопливих фактів про гострі кути, які додадуть вам любові до геометрії:

• 🌟 Золотий трикутник: У рівнобедреному трикутнику із кутами 36°, 72° і 72° (так званому золотому трикутнику) усі кути є гострими, а співвідношення сторін відповідає золотому перетину, що робить його унікальним у математиці та мистецтві.
• 🔍 Гострі кути в зірках: П’ятикутна зірка (пентаграмма) містить гострі кути в 36°, які повторюються в її вершинах, створюючи гармонійну симетрію.
• ⚙️ Механіка: У годинниках стрілки, що утворюють гострий кут (наприклад, о 10:00), допомагають нам швидко оцінити час завдяки чіткій геометричній формі.
• 🌱 Природа і гострі кути: Гострі кути листя багатьох рослин допомагають спрямовувати дощову воду до коренів, оптимізуючи їхнє зволоження.

Ці факти показують, що гострі кути — це не лише числа, а й частина природи, мистецтва та технологій.

Як розпізнати гострий кут на практиці?

Розпізнавання гострого кута — це навичка, яка стане в пригоді як у школі, так і в житті. Ось кілька порад, як це зробити:

1. Порівняння з прямим кутом: Якщо кут виглядає “вужчим” за прямий кут (90°), він, найімовірніше, гострий. Наприклад, кут між двома стінами в кімнаті зазвичай прямий, тож якщо кут менший — він гострий.
2. Використання косинця: Косинець із прямим кутом — чудовий інструмент для порівняння. Якщо ваш кут “ховається” всередині прямого кута косинця, він гострий.
3. Оцінка на око: З досвідом ви почнете інтуїтивно розпізнавати гострі кути, адже вони виглядають “гострішими” і компактнішими.

Практика робить майстра! Спробуйте знайти гострі кути у своєму оточенні: у трикутних вивісках, кріслах чи навіть у формі піци, нарізаної на шматки.

Типові помилки при роботі з гострими кутами

Навіть досвідчені учні можуть припускатися помилок, коли працюють із гострими кутами. Ось найпоширеніші з них:

• Неправильне вимірювання: Іноді транспортир неправильно вирівнюють, що призводить до неточних результатів. Завжди перевіряйте, чи центр транспортира збігається з вершиною кута.
• Плутанина з тупими кутами: Деякі плутають гострі та тупі кути, особливо якщо кут близький до 90°. Пам’ятайте: гострий кут завжди менший за 90°.
• Ігнорування суміжних кутів: Якщо два кути суміжні, а один із них гострий, другий може бути тупим. Це важливо враховувати при обчисленнях.

Щоб уникнути цих помилок, завжди перевіряйте свої вимірювання та використовуйте надійні інструменти, як-от транспортир або косинець.

Гострі кути в тригонометрії: глибше занурення

Для просунутих читачів гострі кути відкривають двері до світу тригонометрії. У гострокутному трикутнику тригонометричні функції (синус, косинус, тангенс) завжди позитивні, що спрощує обчислення. Наприклад, якщо кут дорівнює 30°, то:

• sin(30°) = 0.5
• cos(30°) = √3/2 ≈ 0.866
• tan(30°) = 1/√3 ≈ 0.577

Ці значення допомагають розв’язувати задачі, пов’язані з обчисленням відстаней, висот і кутів у реальному світі, наприклад, у навігації чи будівництві.

Гострі кути також відіграють ключову роль у законі косинусів і законі синусів, які дозволяють знаходити невідомі сторони та кути трикутника. Наприклад, закон косинусів для трикутника зі сторонами a, b, c і кутом C виглядає так:

c² = a² + b² − 2ab·cos(C)

Якщо кут C гострий, cos(C) буде позитивним, що впливає на результат обчислень.

Чому гострі кути важливі?

Гострі кути — це не просто математична концепція, а ключ до розуміння світу. Вони допомагають нам аналізувати форми, будувати міцні конструкції, створювати красиві дизайни та навіть орієнтуватися в просторі. Від трикутних мостів до зірок на небі — гострі кути є всюди, і їхнє вивчення відкриває нові горизонти в математиці та житті.